Navigation in off-road environments is challenging due to their uneven and high-risk terrains. It’s vital to reason over these complex terrains to avoid unsafe or unrecoverable behaviors. We present a diffusion model approach conditioned on local costmaps to generate long-horizon plans for off-road driving. We tested our approach using both pure gaussian noise as well as smart seeding and observe the differences in the outputted trajectories. We evaluate our method through measuring the average loss over the training period and observed that the random-seeding approach achieves convergence and can diffuse viable trajectories.
The two key insights here are:
- Replacing demonstration data with “demonstrations” generated by querying a trajectory library against a costmap generated via inverse reinforcement learning.
- “Smart-seeding” the diffusion initializaion, which requires a custom noise scheduler.
Currently, the smart-seeding approach seems to not converge or perform well, likely due to a implementation error or issues with the reverse diffusion. Our code can be found here.
Motivation

- Navigating in off-road environments is challenging:
- Tough terrain - ditches, mud, foliage, puddles
- Elevation challenges - slope and height irregularities
- Sampling-based local planners are popular:
- We use MPPI - we roll out random actions, evaluate them on a costmap, and choose the best trajectory
- It is difficult to do dense sampling over long-horizons
- Lots of trajectories will be in high-cost regions (imagine you’re on a narrow trail and have to evaluate a bunch of samples that crash into the trees on the side)
- This esults in a lot of wasted compute
What if we could learn the best distributions to sample paths from given current environment conditions?
Approach
Architecture
More details coming soon after we work out some bugs but, at a high level, we follow an approach similar to NoMaD but without the goal-masking/conditioning element. Additionally, we condition on costmaps instead of FPV RGB images.

Initial Results
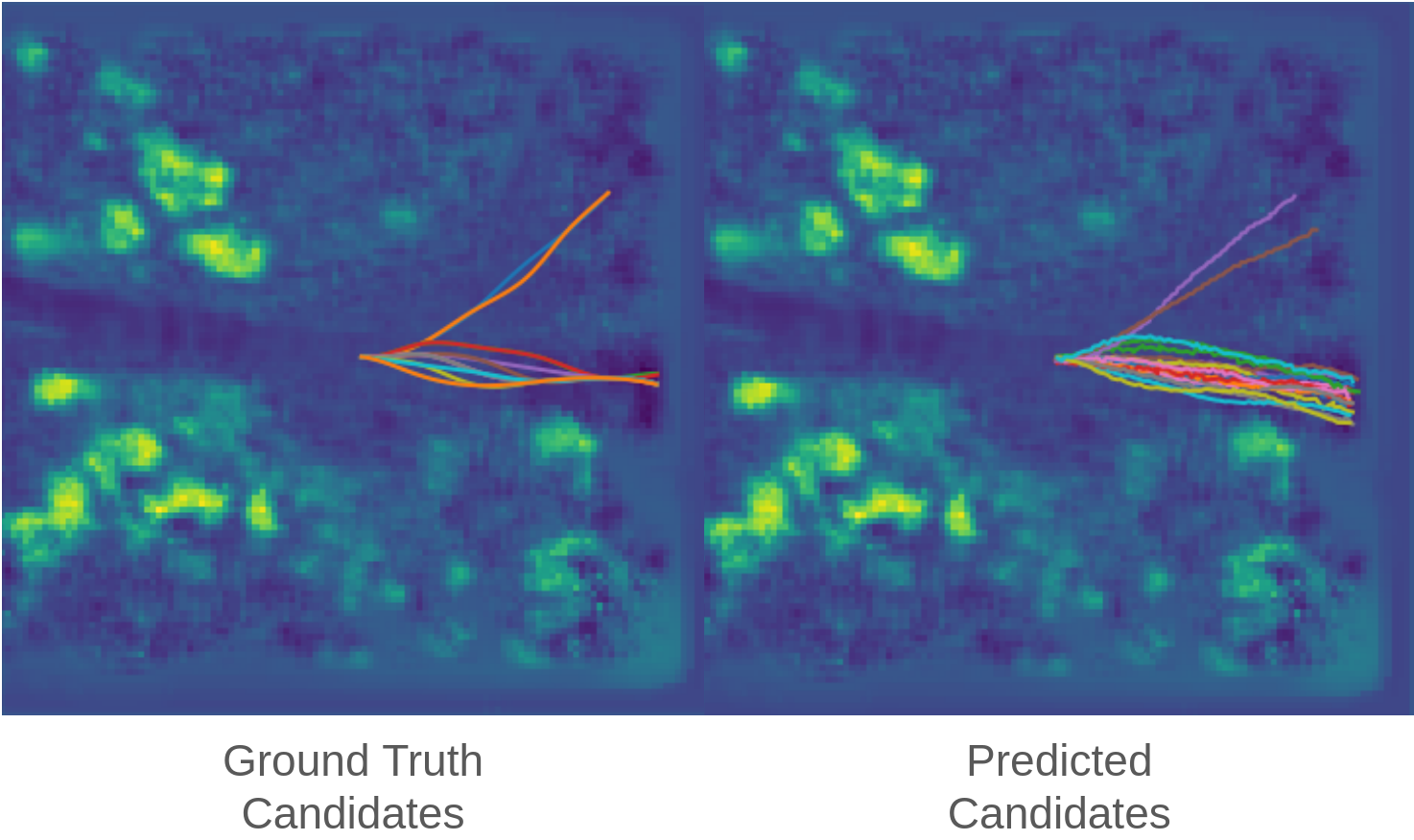
We show that we can diffuse reasonably feasible trajectories conditioned on the costmaps.

In some cases, even intuitive multi-distribution paths are predicted. For example, the result at a fork in the road is shown below.